叉乘的几何意义（探讨叉乘在几何中的重要性）

在数学和物理学中，叉乘是一种重要的向量运算，通常用符号“×”表示。它具有深刻的几何意义，可用于解释向量之间的关系，尤其在三维空间中。下面将讲解叉乘的几何意义，详细介绍其定义以及如何应用于解决实际问题。

1、叉乘的定义

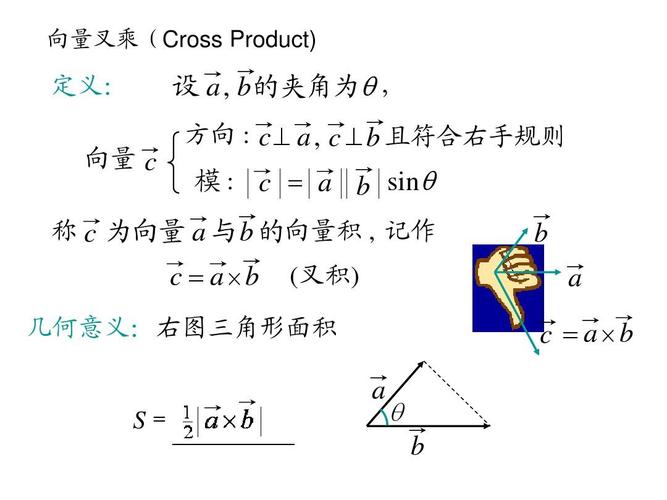
叉乘是两个向量之间的向量积，通常由以下公式定义： $\vec{A} \times \vec{B} = |\vec{A}| \cdot |\vec{B}| \cdot \sin(\theta) \cdot \hat{n}$ 其中，$\vec{A}$和$\vec{B}$是待叉乘的两个向量，$|\vec{A}|$和$|\vec{B}|$分别是它们的模长，$\theta$是$\vec{A}$和$\vec{B}$之间的夹角，$\hat{n}$是一个垂直于$\vec{A}$和$\vec{B}$所在平面的单位向量。

2、叉乘的方向

叉乘的一个重要几何意义是确定了结果向量的方向。结果向量$\vec{C} = \vec{A} \times \vec{B}$垂直于$\vec{A}$和$\vec{B$所在的平面。右手法则可用于确定$\vec{C$的方向，其中拇指指向$\vec{A}$，食指指向$\vec{B$，中指即为$\vec{C$的方向。

3、面积和体积

叉乘还可以用来计算平行四边形的面积和行星立体角体积。如果两个向量$\vec{A}$和$\vec{B}$共同定义一个平行四边形，那么该平行四边形的面积等于$|\vec{A} \times \vec{B}|$。

4、角度和正弦定理

叉乘还有助于解决三角形的角度和边长问题。通过叉乘，可以推导出正弦定理，这是三角学中的重要定理，用于关联三角形的边和角。

5、应用案例

叉乘在实际问题中有广泛的应用，例如，地理学家可以使用叉乘来计算地球上某一点的纬度和经度的变化率，从而理解地球表面的动态过程。工程师可以使用叉乘来计算力矩，从而设计稳定的结构。计算机图形学中，叉乘用于确定法向量，用于着色和渲染三维对象。

叉乘是一种强大的向量运算，具有深刻的几何意义。它不仅可以用来确定向量的方向，还可以用于计算面积、体积、角度和边长。在各个领域中，叉乘都有广泛的应用，因此，了解叉乘的几何意义对数学、物理学和工程学等领域的学生和专业人士来说都是至关重要的。

在许多问题中，叉乘可以提供有关向量之间关系的关键信息，有助于解决复杂的问题。通过深入理解叉乘的几何意义，我们能更好地理解世界，并在各种领域中做出有影响力的决策。