向量叉乘的几何意义(向量叉乘的几何解释)
向量叉乘,也称为矢量叉积或叉积运算,是线性代数中的重要概念,用于描述向量之间的关系和几何性质,这一概念在许多领域,如物理学、工程学和计算机图形学中都扮演着关键的角色。下面将讲解向量叉乘的几何意义,以及它在不同领域的应用。

向量叉乘的定义和公式
向量叉乘是两个向量之间的一种运算,通常用符号“×”表示。给定两个三维向量A和B,它们的叉乘结果记作A × B。其计算公式如下:
其中,|A|和|B|分别表示向量A和B的模长,θ表示A和B之间的夹角,n是一个垂直于A和B所确定的平面上的单位向量。
向量叉乘的几何意义
向量叉乘的几何意义在于它可以用来计算两个向量之间的垂直性和平行性。具体来说,以下是向量叉乘的几何意义:
1、垂直性
当两个向量A和B之间的叉乘A × B等于零时,这表示它们是垂直的,这是因为sin(θ)等于零,只有当θ为零或π时才能使sin(θ)等于零,这时A和B是共线的,即平行或反向。
2、平行性
如果A × B的结果不为零,那么A和B不是共线的,它们之间存在一定的夹角θ。通过叉乘运算,我们可以得到一个新的向量,该向量垂直于A和B所确定的平面,并且其模长等于A和B构成的平行四边形的面积。
3、向量叉乘的应用领域
向量叉乘在多个领域中具有广泛的应用,包括:
1、物理学
在物理学中,向量叉乘常用于描述力矩、磁场和角动量等物理量的方向和性质,例如,当一个力作用在一个物体上时,力矩可以通过叉乘计算,从而确定物体的旋转方向。
2、工程学
在工程学中,向量叉乘用于计算力的分布、扭矩、应力分布和流体动力学等问题。工程师使用叉乘来优化结构设计和分析材料的性质。
3、计算机图形学
在计算机图形学中,向量叉乘用于计算三维图形中的法向量,以确定光照效果和渲染,这有助于创建逼真的三维场景和动画。
向量叉乘是一个强大的工具,用于理解向量之间的关系和几何性质。它在数学、物理学、工程学和计算机图形学等领域都具有广泛的应用。通过分析叉乘的几何意义,我们能够更好地理解和应用这一重要概念,以解决各种实际问题。
总的来说,向量叉乘的几何意义在于帮助我们理解向量之间的相对方向关系,尤其在描述垂直性和平行性方面具有重要作用,这一概念的应用影响了多个领域,为解决各种复杂问题提供了有力的数学工具。
相关阅读
-
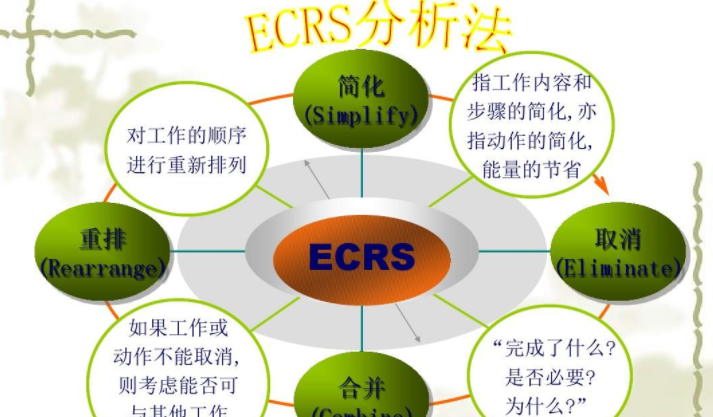
ECRS四大原则,即取消(Eliminate)、合并(Combine)、重排(Rearrange)、简化(Simplify),是企业工业工程学中程序分析的四大原则,用于对生产......
-
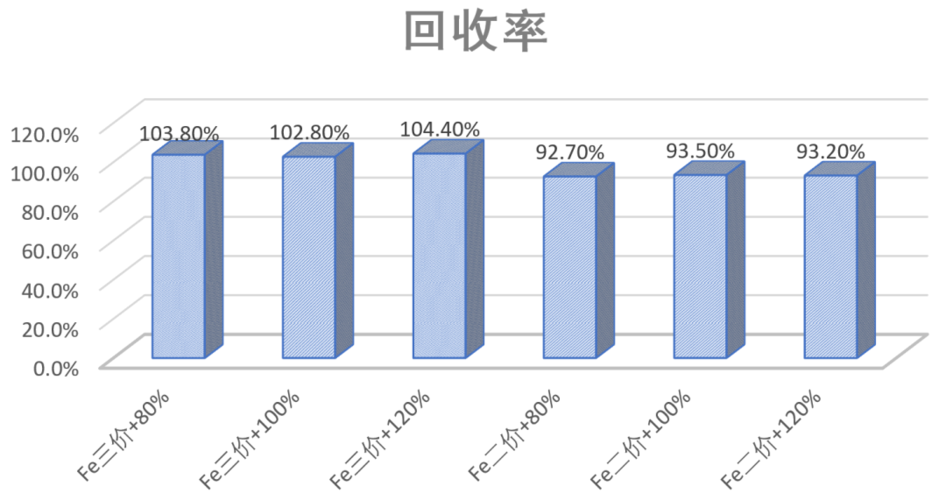
加标回收率的意义在于它为我们提供了一种评估和提高分析方法准确性的工具,有助于确保数据的可靠性和精确性。加标回收率的正确计算和维护对于许多领域至关重要,它有助于保护公共健康、确......
-

非遗传承具有重要的文化、社会和经济意义。它不仅有助于传承文化记忆,弘扬国家精神,促进经济发展,还有助于促进跨文化理解。非遗传承是一项不可或缺的任务,需要得到充分的支持和重视,......
-

教育具有深远的意义和巨大的价值,既有助于个人的成长和发展,也有助于社会的繁荣和进步。无论从知识传承、经济增长、社会公平还是文化传承的角度看,教育都扮演着不可或缺的角色,因此,......
-
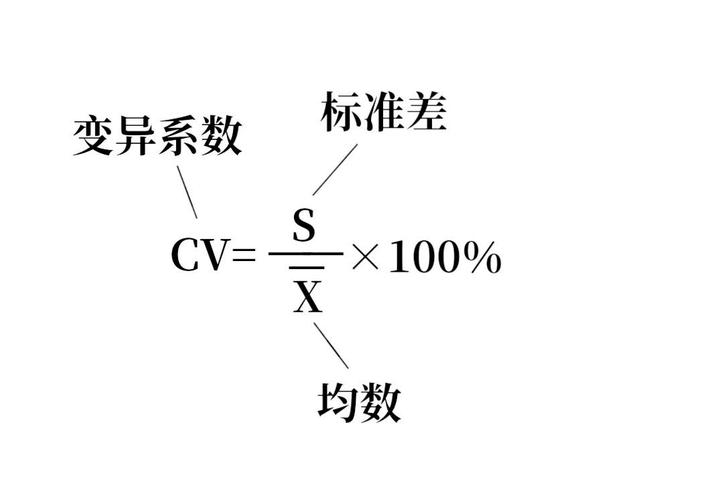
通过计算变异系数,我们可以了解到数据的离散程度大小。较大的变异系数表示数据波动性较高,较小的变异系数表示数据波动性较低。同时,在比较不同数据集之间的离散程度时,变异系数也是一......
-

香港澳门回归的意义在于恢复中国主权、维护地区稳定、促进经济繁荣、加强国际地位以及保护文化遗产,这一历史性事件在中国和国际舞台上都具有深远的影响,为这两个特别行政区的未来发展提......
发表评论


