四阶行列式的计算方法(讲解四阶行列式求解的步骤和公式)
四阶行列式的计算方法:第1步:把2、3、4列加到第1 列,提出第1列公因子 10,化为 1 2 3 4 1 3 4 1 1 4 1 2 1 1 2 3 第2步:第1行乘 -1 加到其余各行,得 1 2 3 4 0 1 1 -3 0 2 -2 -2 0 -1 -1 -1 第3步:r3 - 2r1,r4+r1,得 1 2 3 4 0 1 1 -3 0 0 -4 4 0 0 0 -4 所以行列式 = 10* (-4)*(-4) = 160。下面将介绍四阶行列式的计算方法,以及其在实际问题中的应用。

一、四阶行列式的定义:
四阶行列式是一个4x4矩阵中元素的特殊组合,用来表示线性方程组的一些性质。其一般形式如下:
|A| = a11 * a22 * a33 * a44 + a12 * a23 * a34 * a41 + a13 * a24 * a31 * a42 + a14 * a21 * a32 * a43 - a14 * a23 * a32 * a41 - a13 * a22 * a34 * a41 - a12 * a21 * a33 * a44 - a11 * a24 * a31 * a42
其中,a11、a12、a13、a14等表示4x4矩阵A中的元素。
二、计算方法:
计算四阶行列式可以使用展开定理或者矩阵的辅助行列式方法。以下是展开定理的步骤:
1、选择第一行或第一列的元素(通常选择第一行),以a11为例。
2、用a11乘以它所在行和列以外的元素的2x2子矩阵的行列式值,得到a11 * M11。
3、重复上述步骤,分别取a12、a13、a14为第一行的情况,得到a12 * M12、a13 * M13、a14 * M14。
4、最后将所有这些结果相加,即可得到四阶行列式的值:|A| = a11 * M11 + a12 * M12 + a13 * M13 + a14 * M14。
三、举例: 假设有一个4x4矩阵A如下:
A = | 2 1 3 4 | | 0 2 1 5 | | 3 1 0 2 | | 1 0 4 3 |
我们可以使用上述计算方法来计算其四阶行列式:
|A| = 2 * | 2 1 5 | | 1 0 2 | - 0 * | 0 1 5 | | 1 4 3 | + 3 * | 0 2 1 | | 1 0 2 | - 4 * | 0 2 1 | | 1 4 3 |
然后,我们计算这些2x2子矩阵的行列式值,代入公式中,最终得到四阶行列式的值。
四、应用领域:
四阶行列式的计算方法在很多领域都有应用,例如,在工程中,它可用于解决刚体力学问题,计算刚体的转动惯量。在经济学中,它可用于构建数学模型,分析经济变量之间的关系。此外,四阶行列式还在图像处理、统计学和计算机图形学等领域中有广泛的应用。
四阶行列式的计算方法是线性代数中的重要内容,它在数学和工程等领域有广泛的应用。通过展开定理,我们可以计算任意4x4矩阵的行列式值,从而解决各种实际问题。无论是解决工程问题,还是分析经济数据,四阶行列式都是一个有力的工具,为我们提供了更深入的数学理解和解决复杂问题的能力。
相关阅读
-

各位朋友们好,假如你对四阶魔方还原公式,和四阶魔方还原公式口诀是什么不是很清楚,没关系,今天小编就为大家解答一下。希望可以帮助到各位,下面就来解答关于四阶魔方还原公式的问题,......
-

各位朋友们好,如果你对四阶魔方还原,和如何还原四阶魔方不是很清楚,今天小编给大家解答一下你们心中的疑问。希望可以帮助到有需要的朋友,下面就来解答关于四阶魔方还原的问题,下面我......
-

各位朋友们好,若是你对四阶魔方公式,与魔方4阶公式有哪些不是很了解,没关系,今天小编就为大家解答一下。希望可以帮助到有需要的朋友,下面就来解答关于四阶魔方公式的问题,下面我们......
-
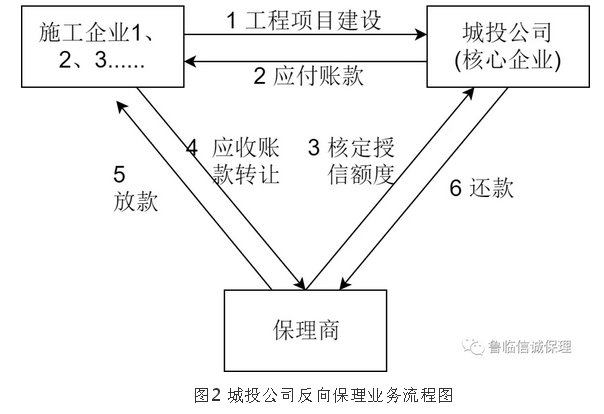
保理支付工程款是指在工程建设领域,承包商通过与保理商签订保理合同,将其应收账款转让给保理商,从而获得资金融通的一种方式。保理商在受让应收账款后,负责向债务人(业主或总包方)催......
-

F0值的概念为灭菌过程赋予一个产品121℃下的等效灭菌时间。具体来说,F0值是标准灭菌时间,在灭菌过程中,只要记录被灭菌物品的温度与时间,就可以通过公式算出F0值。F0值的意......
-

棕白色大熊猫叫七仔。这是世界上唯一一只棕白色的大熊猫,这只大熊猫是在陕西佛坪国家级自然保护区三观牌坊沟发现的,住在秦岭大熊猫繁育研究中心。...
-
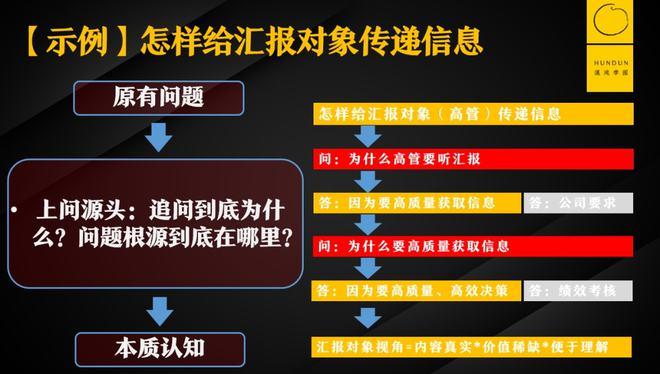
汇报对象是指你要向谁汇报,一般指上级或者直接主管领导。汇报对象其实就是你向你的直接领导汇报你的工作内容,怎么安排事情,怎么分配工作内容,一切工作的运转境况,包括一些小的细节,......
-

衍生,汉语词语,意思指蕃衍生息;一种较简单的化合物中的原子或原子团被其他原子或原子团置换而生成较复杂的化合物。...
-

delete的读音是:英dɪˈliːt美dɪˈlit。delete是一个英文单词,动词,作动词时意思为“删除”。它有多种发音方式,英式发音为dɪˈliːt,美式发音为dɪˈl......
发表评论


