变异系数的意义（了解变异系数及其应用）

变异系数（Coefficient of Variation，简称CV）是统计学中一个重要的概念，用来衡量数据集的相对离散程度。它是标准差与均值的比值，通常以百分数表示。变异系数不仅是一种描述性统计量，还是数据分析和比较的有力工具，其重要性不可低估。

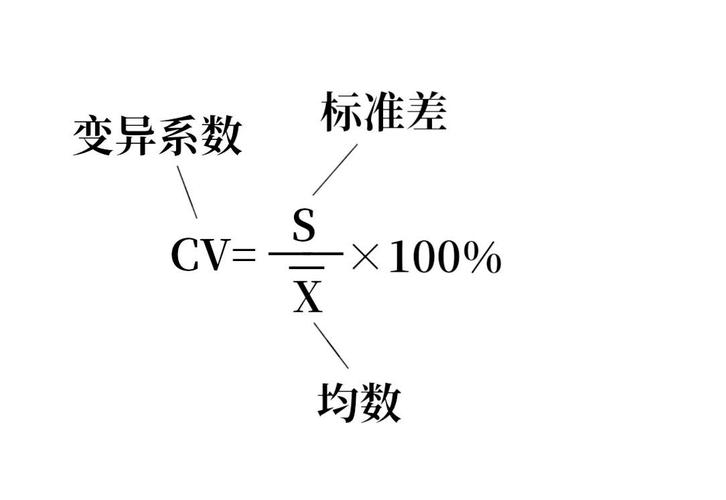
变异系数的计算

变异系数的计算非常简单，可以用以下公式表示：

$CV = \left( \frac{标准差}{均值} \right) \times 100\%$

其中，标准差代表数据的离散程度，均值则表示数据的中心趋势。

变异系数的意义

相对比较数据的离散程度： 变异系数允许我们比较不同数据集的离散程度，而不受均值的影响。假设有两个投资组合A和B，A的年均回报率为8%，标准差为12%，而B的年均回报率为10%，标准差为15%。虽然B的回报率更高，但变异系数显示，B的回报波动更大，投资风险较高，这对于风险管理和决策制定非常重要。

适用于不同量纲的数据： 变异系数是一个相对指标，因此可以用于不同量纲的数据集，这使得我们可以比较不同领域的数据，如温度、股票回报率、销售额等。

评估数据的一致性： 变异系数还可用于检验数据的一致性。当CV较低时，数据较一致，适合用于建模和预测。当CV较高时，数据可能存在较大的波动，需要谨慎分析。

支持决策制定： 在业务和经济领域，变异系数有助于决策制定，例如，一个公司可能会比较不同产品线的利润变异系数，以确定哪个产品线的风险更低或更可靠。

变异系数的示例

为了更好地理解变异系数的意义，考虑以下示例：

假设有两个城市A和B，它们的月均降水量数据如下：

• 城市A：均值 = 60毫米，标准差 = 10毫米

• 城市B：均值 = 40毫米，标准差 = 5毫米

计算它们的变异系数：

• 城市A的CV = $\left(\frac{10}{60}\right) \times 100\% = 16.67\%$

• 城市B的CV = $\left(\frac{5}{40}\right) \times 100\% = 12.5\%$

通过比较变异系数，我们可以得出结论，城市A的降水量波动相对较大，而城市B的降水量波动相对较小，这对于气象预测和水资源管理都具有重要意义。

变异系数是一个强大的统计工具，用于衡量数据的相对离散程度，支持决策制定和数据比较。无论是在科学研究、经济分析还是其他领域，都可以借助变异系数更好地理解数据的特性和波动性。要更好地利用这一工具，我们应该始终将其考虑在内，以提高数据分析的质量和可信度。